I previously showed some fun classical logic proofs in Haskell, thanks to the Curry-Howard correspondence.

This post will show how a simple proof works in Logic, Type Theory, and Category Theory: given A ∧ (B ∧ C), prove (A ∧ B) ∧ C.

Logic

In logic, there are several systems that allows us to reason about propositions. One of them is the natural deduction system and is defined using introduction and elimination rules. For each connective, or operator, we will have at least one of each introduction and elimination rules.

For example, conjunction (∧) has one introduction rule:

 A   B
------- (∧i)
 A ∧ B

which means, if we know A and B, then we can use the introduction rule (∧i) to deduce the proposition A ∧ B.

There are two elimination rules for ∧:

A ∧ B                 A ∧ B
----- (∧e1)           ----- (∧e2)
  A                     B

which means, if we know A ∧ B, we can obtain A or B if we use the elimination rules ∧e1 or ∧e2.

So, if we wanted to prove the conclusion(A ∧ B) ∧ C) from the hypothesis A ∧ (B ∧ C), we would have to: 1. obtain an A by using ∧e1 on the hypothesis 2. obtain a B ∧ C by using ∧e2 on the hypothesis 3. obtain a B by using ∧e1 on (2) 4. obtain a C by using ∧e2 on (2) 5. obtain a A ∧ B by using ∧i on (1) and (3) 6. reach the conclusion (A ∧ B) ∧ C by using ∧i on (5) and (4)

In natural deduction, it looks like this:

A ∧ (B ∧ C)          A ∧ (B ∧ C)
----------- (∧e1)   ------------- (∧e2)
     A                   B ∧ C
     .              --- (∧e1)  --- (∧e2)
     A               B          C
  --------------------- (∧i)    .
          A ∧ B                 C
     ------------------------------- (∧i)
                (A ∧ B) ∧ C

Type Theory

The Curry-Howard correspondence tells us that conjunction translates to pairs in type theory, so we'll switch notation to Haskell's tuple type, using the following notation: - Types: capital letters A B C D - Terms: lowercase letters a b c d - Tuple Types: (A, B) for the tuple A B - Tuple Terms: (a, b) for the tuple a b of type (A, B)

Typed lambda calculus has a deduction system as well. Tuple introduction looks very similar to ∧i:

  a : A    b : B
------------------ ((,)i)
 (a, b) : (A, B)

which means, given a term a of type A and a term b of type B, then we can obtain a term (a, b) of type (A, B). Note that we no longer need to say "given we know A and B", since the existence of a term of each type is enough to form the tuple.

Similarly, there are two elimination rules:

  (a, b) : (A, B)                  (a, b) : (A, B)
------------------- ((,)e1)      ------------------- ((,)e2)
       a : A                            b : B

which means, given a tuple (a, b) of type (A, B) we can obtain a term a or b of type A or B.

If we translate the proposition above, then we have to prove ((A, B), C) from (A, (B, C)).

(a, (b, c) : (A, (B, C))          (a, (b, c)) : (A, (B, C))
------------------------ ((,)e1)  ------------------------- ((,)e2)
         a : A                         (b, c) : (B, C)
           .                        ------- ((,)e1) ------- ((,)e2)
         a : A                       b : B           c : C
  ----------------------------------------- ((,)i)     .  
                (a, b) : (A, B)                      c : C
            -------------------------------------------------- ((,)i)
                        ((a, b), c) : ((A, B), C)

The form is identical to the logic proof, except we have terms and the rules use (,) instead of ∧.

Haskell Proof

We can write the same thing in Haskell:

assoc :: (a, (b, c)) -> ((a, b), c)
assoc (a, (b, c)) = ((a, b), c)

However, this takes advantage of a powerful Haskell feature known as pattern matching.

Given the proof above, it's easy to noice that (,)i is exactly the tuple constructor, (,)e1 is fst and (,)e2 is snd. Knowing this, and looking at the proof above, we could say, given hypothesis h = (a, (b, c)) : (A, (B, C)), we can obtain:

1. a : A from fst h
2. (b, c) : (B, C) from snd h
3. b : B from fst (snd h)
4. c : C from snd (snd h)
5. (a, b) : (A, B) from (fst h, fst (snd h))
6. ((a, b), c) : ((A, B), C) from ((fst h, fst (snd h)), snd (snd h))

So, in Haskell:

assoc' :: (a, (b, c)) -> ((a, b), c)
assoc' h = ((fst h, fst (snd h)), snd (snd h))

This is a neat effect of the Curry-Howard correspondence: proofs are programs. So, once we write the proof, we also have the program. We could even write the program and then extract the proof -- it's really the same thing.

Category Theory

The Curry-Howard-Lambek extends the correspondence to include CT as well. The correspondence connects propositions to objects, arrows to implication, conjunction to categorical products, etc.

While in logic we said "given a proof of A", and in type theory we said "given a term of type A", the only way we can do the same in CT is to say "given an arrow from the terminal object T to A, f : T → A". This works because the terminal object represents True / Unit in logic / type theory, so it means "given we can deduce A from True", or "given we can obtain a term a : A from () : ()".

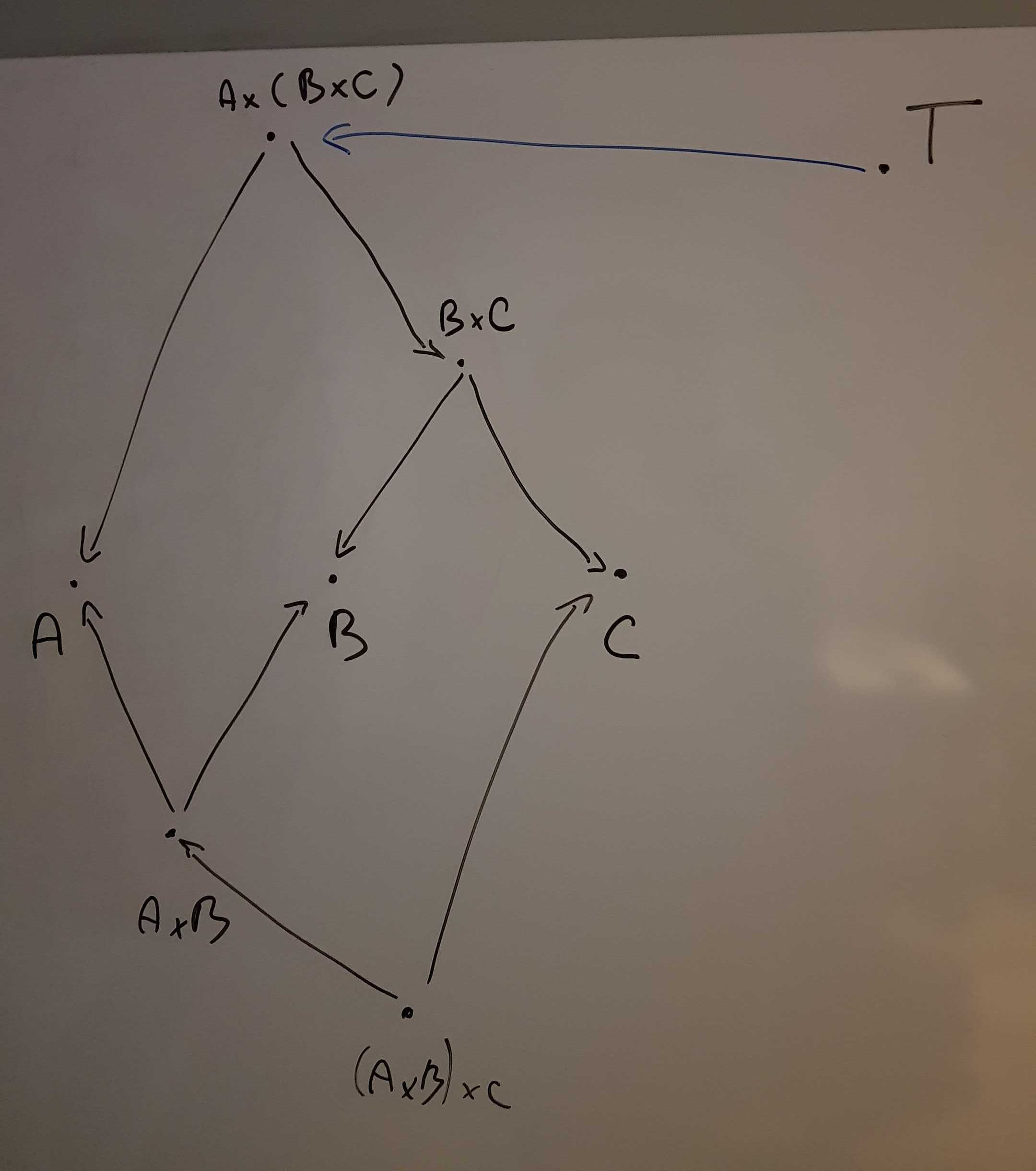
Armed with this, we can now express the same problem in CT terms: - given an arrow h : T → (A × (B × C)) - obtain an arrow p : T → ((A × B) × C))

Before we begin, let's review what a product is: - given A × B, we know there are two arrows p : A × B → A and q : A × B → B, which we will write as <p, q> - given A × B is the product of A and B, and C is an object with two arrows p' : C → A and q' : C → B, there exists an unique arrow m : C → A × B such that p ∘ m = p' and q ∘ m = q'

Also, remember that we can compose any two arrows f : A → B and g : B → C via g ∘ f.

Now we are ready for the proof:

T is the terminal object, and t : T → A × (B × C) is what we start with. We need to be able to obtain an arrow t' : T → (A × B) × C).

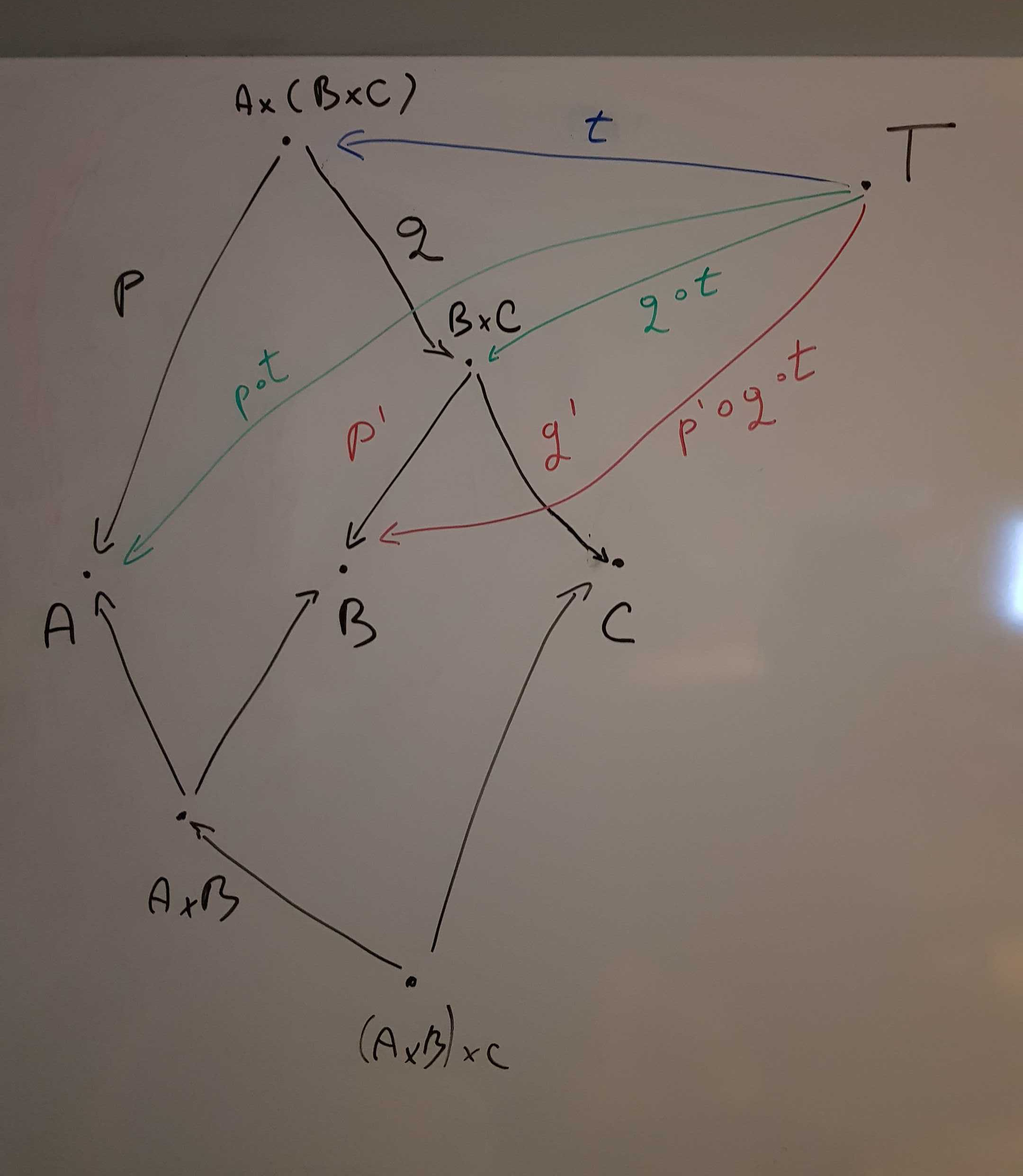
By product A × (B × C), we know there exists p : A × (B × C) → A and q : A × (B × C) → B × C.

By composition, we can obtain the arrows p ∘ t : T → A and q ∘ t : T → B × C.

By product B × C, we know there exists p' : B × C → B and q' : B × C → C.

By composition, we can obtain the arrow p' ∘ q ∘ t : T → B.

So now, we have the following arrows: - p ∘ t : T → A - p' ∘ q ∘ t : T → B

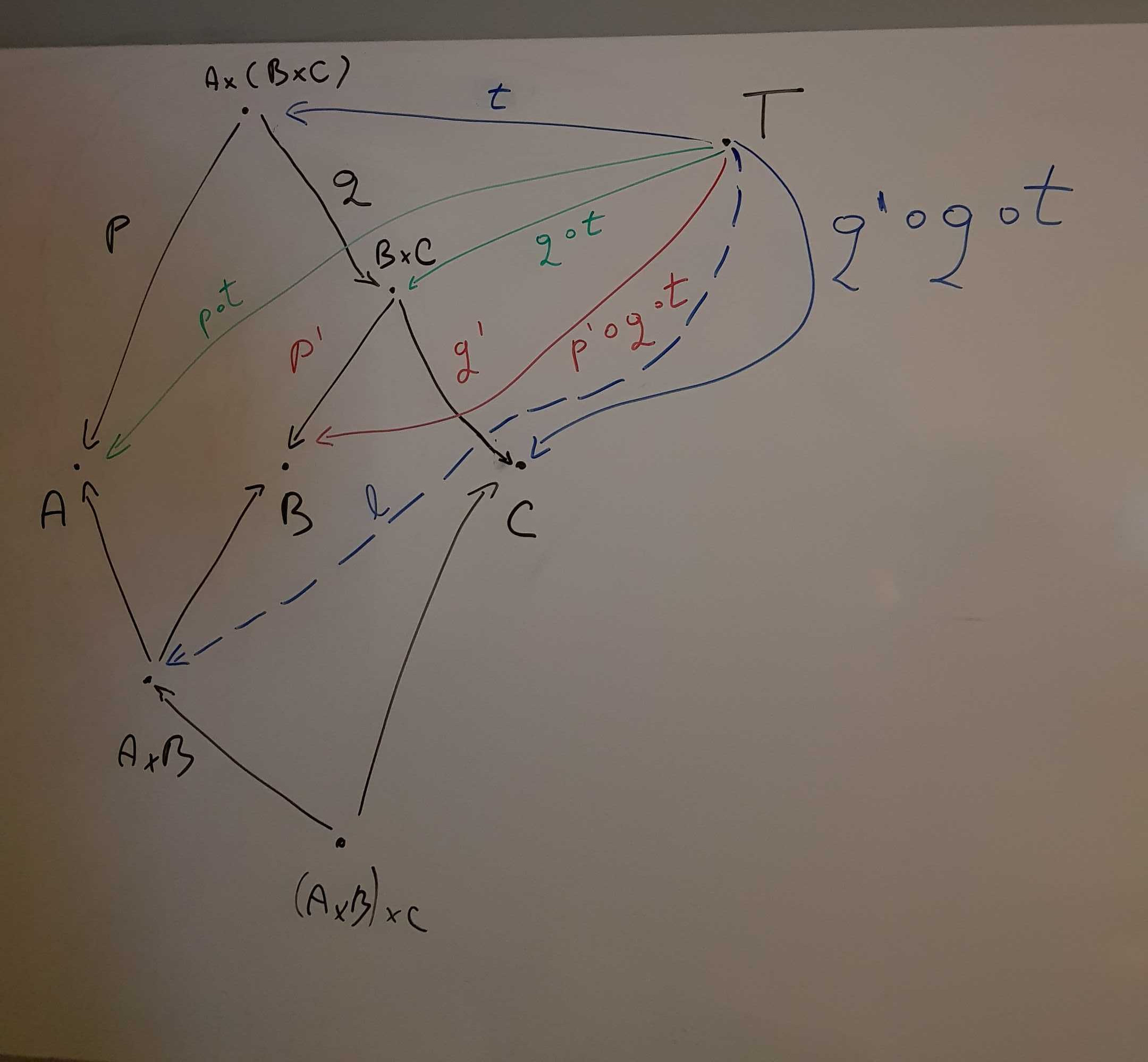
By definition of product, since we know A × B is the product of A and B, and since we have the arrows T → A and T → B, then we know there must be an unique arrow which we'll name l : T → A × B.

By composition we can obtain the arrow q' ∘ q ∘ t : T → C.

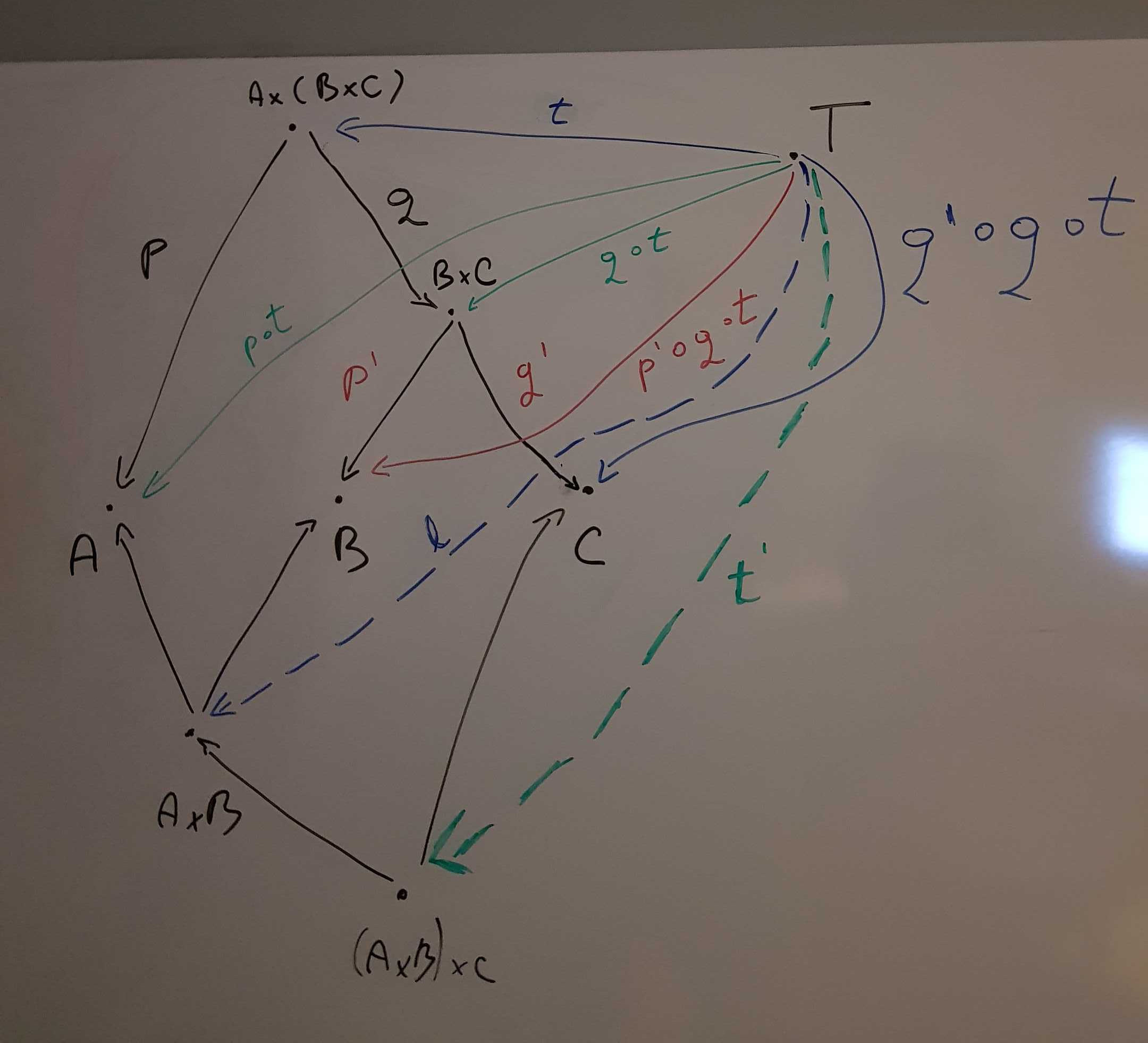
Similarly to the step before, by definition of product, since we know (A × B) × C is a product of A × B and C, and since we have the arrows l : T → A × B and q' ∘ q ∘ t : T → C, then there must exist an unique arrow t' : T → (A × B) × C.

Note: there are, in fact, as many arrows T → (A × B) × C as are elements in (A × B) × C, but t' is the unique one derived from the initial arrow, t.

Edit: See this twitter thread for a whiteboard proof of sum associativity.

Back to Haskell

If we follow the CT arrows as we followed the logic proof: - we could rewrite the l : T → A × B arrow as <i,j> : T → A × B, where i = p ∘ t : T → A and j = p' ∘ q ∘ t : T → B. - we already have k = q' ∘ q ∘ t : T → C

So, if instead of t we write a_bc to denote our hypothesis, or inputs, let's look closer at what i, j and k are: - i is p ∘ t, which is the left projection of the premise, or fst a_bc

You may ask: Why?!? Well, p ∘ t means p after t. In our case, t represents the input, so it's equivalent to a_bc, and p is the left projection, which is equivalent to fst. Keep in mind that a ∘ b ∘ c means c first, then b, then a when reading the following.

• j is p' ∘ q ∘ t, which is fst (snd a_bc)
• l = <i,j>, so l = (fst a_bc, fst (snd a_bc))
• k is snd (snd a_bc)
• the result, T → (A × B) × C is < <i,j>, k > = ((fst a_bc, fst (snd a_bc)), snd (snd a_bc))

If we look back at the Haskell definition: assoc a_bc = ((fst a_bc, fst (snd a_bc)), snd (snd a_bc))

Which means we reached the same implementation/proof, again.

Edit: Thank you to Bartosz Milewski and GhiOm for their early feedback.